Turing machine is a computational model that has unrestricted memory. It is more general purpose and accurate compared to automata.
Definition of a Turing Machine

Read as (Q, Sigma, Gamma, delta, q0, q_accept, and q_reject)
Configuration of TM
- The configuration of TM represents:
- current state (q)
- current content (first letter in v)
- and current location (evinced by u and v)
- *u q v: the left tape + q + the right tape
- e.g. 0101 q5 01111
- the q represents the first tape block in the right tape (v)
- this means q5 indicates the state of the block that contains ‘0’
Turing machine M accepts input $w$ if a sequence of configurations $C_1$, $C_2$, …, $C_k$ exists, where:
- $C_1$ is the starting configuration
- Each $C_i$ yields $C_(i+1)$
- $C_k$ is an accepting configuration
Language of M
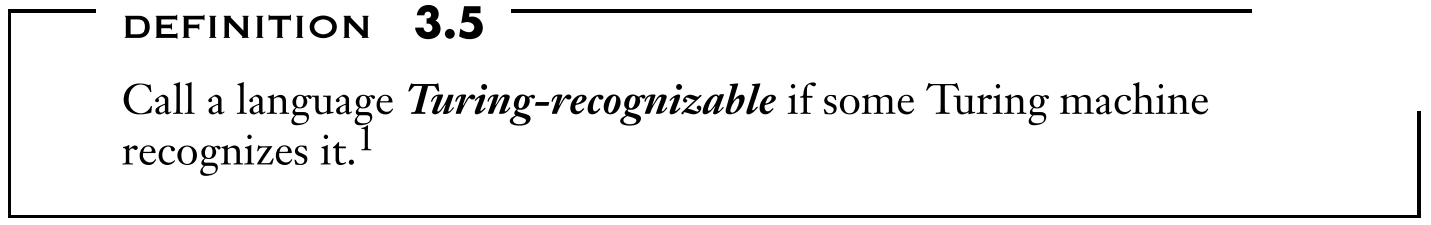
The language of M is the set of all strings that M accepts.
If an input w is accepted by a TM, then w belongs to the language of the TM (or the language recognized by the TM).
Recognize means, for an input w $\in$ the language, M accepts it, aka finishing in the accept state. While for an input w $\not\in$ the language, M can either fall into a state of accept or looping.
When a TM is given input, three outcomes are possible: accept, reject, and loop.
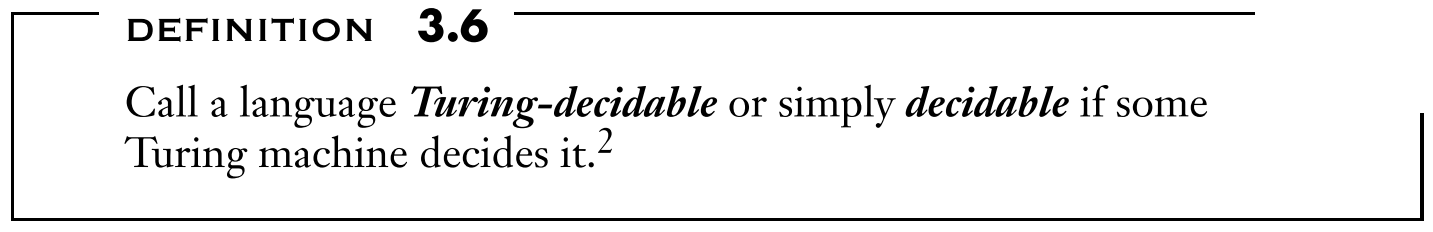
A decider is a TM that halts on all inputs, meaning never loops.
All deciders are recognizers.
Decide means, for an input w $\in$ the language, M accepts it. While for w $\not\in$ the language, M rejects it.
Therefore, all Turing-decidable languages are Turing-recognizable. We can consider a decidable language to be a special case of the recognizable languages.
Practicing Making Turing Machines
When designing TMs, we usually use higher-level descriptions with natural language instead of defining them using formal descriptions, which can be very tedious. However, the high-level descriptions of a TM is just a shorthand representation of its corresponding low-level sets of instructions.
We will work on a classic problem of Turing Machine:
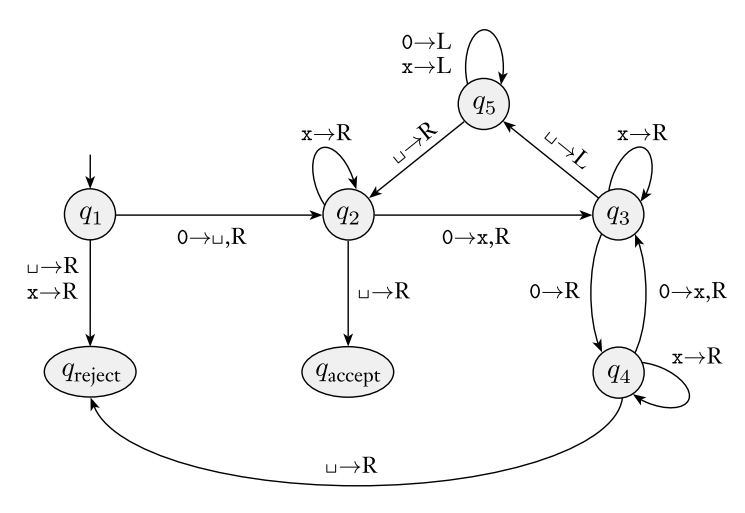
design a TM that decides the language A = {$0^{2^n}$ | $n >= 0$}. In natural language, a language consisting of strings of 0s whose length is a power of 2.
As a programmer and a noob in TOC, my instant intuition was to implement a counter that counts the number of 0s. However, Turing Machines cannot count! Our solution here would be, using two states to represent an even and an odd condition, and switch back and forth.
Let’s first define this TM at a higher level:
M = “On input string w:
- Sweep from left to right, crossing off every other 0. (From left to right, cross of an unmarked 0, then skip one block, and cross of the one after and so on.) e.g. 00000 -> 0x0x0
- If in stage 1 and the tape contains a single 0, accept
- If in stage 2 and the tape contains more than a single 0 and the number of 0s is odd, reject.
- Return the head to the left-hand end of the tape.
- Go back to stage 1.”
And here is how you can define it in a formal way:
M = {Q, $\Sigma$, $\Gamma$, $\delta$, $q_0$, $q_\text{accept}$, $q_\text{reject}$}
Q = {${q_0, q_1, q_2, q_3, q_4, q_5}$}
$\Sigma$ = {0}
$\Gamma$ = {0, x, $\sqcup$}
Now, the transition function $\delta$ is a tough one, but the idea is easy: using two (or more) states to represent even and oddity.
You are not required to build a TM’s transition function completely from scratch, but it is good to build a new intuition, one that is very different from both math and coding!
For more practice, you can look into the book: https://cs.brown.edu/courses/csci1810/fall-2023/resources/ch2_readings/Sipser_Introduction.to.the.Theory.of.Computation.3E.pdf#page=197
Conclusion
Anyways, this is the theoretical and formal aspect of a Turing Machine. It might appear to be a little more complicated than the Turing Machine you already learned or seen from YouTube videos: https://www.youtube.com/watch?v=dNRDvLACg5Q by Computerphile. I encourage you to watch it, for building up that intuition and visualization!
Next topic, we will dive into the variations of different Turing Machines, and our proofs that these variations are all equivalent to the Universal Turing Machine in terms of computation power.