Question: Does a Turing Machine that has the ability to stay put have the same computing power as a regular Turing Machine? Meaning, does a TM with a varying transition $\delta$: Q x $\Gamma$ $\rightarrow$ Q x $\Gamma$ x {L, R, S}, in which S is an extra direction that represents stay, works the same as a universal TM?
After reading another paragraph, you will know the answer instantly!

Variants of TMs are alternative definitions of TM. Any reasonable variant has the same computing power with the universal TM (UTM). Turing Machines are robust, meaning they have a high degree of invariance to changes in the model definition.

The answer to the opening question: YES, a UTM and a TM that can stay put have the exact same computing power. We can always simulate a stay-put TM with a regular TM, by simply adding an extra transition state to each existing state, telling the head to move right. Then at the transition state, move the head left so that it returns to the original position, and the machine stays put indeed. In other words, we do so by replacing each stay put transition with two transitions: one that moves to the right and the second back to the left.

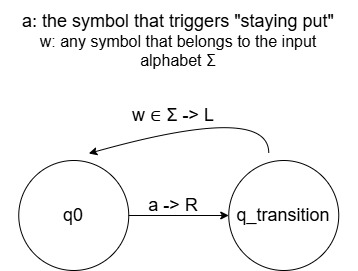
figure 1

Multi-Tape Turing Machines

Multi-tape TMs look like this (M):

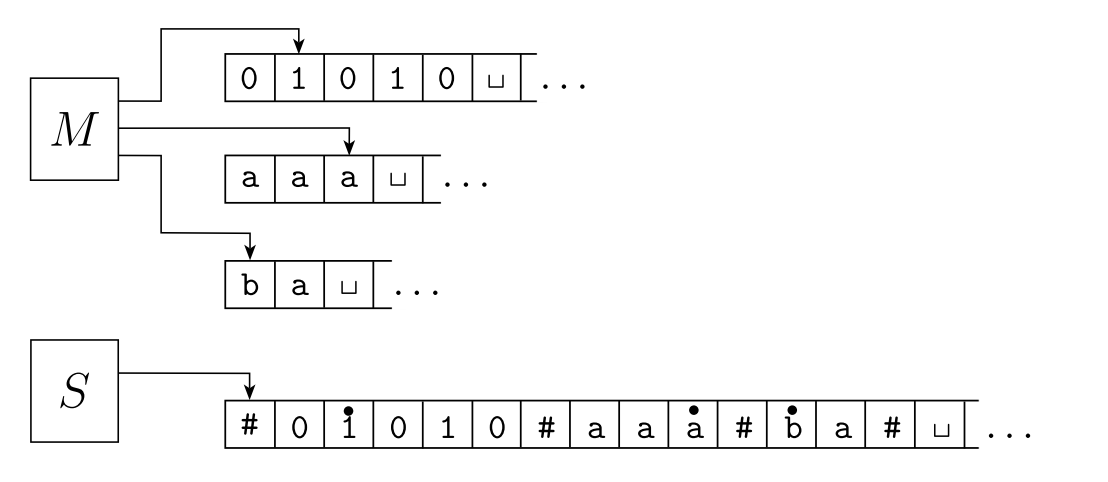
figure 2
The first tape is the input tape, while the other tapes are empty tapes that start with the blank symbol $\sqcup$.

Multi-tape TM’s definition is not much different than a universal TM, except the transition function $\delta$:

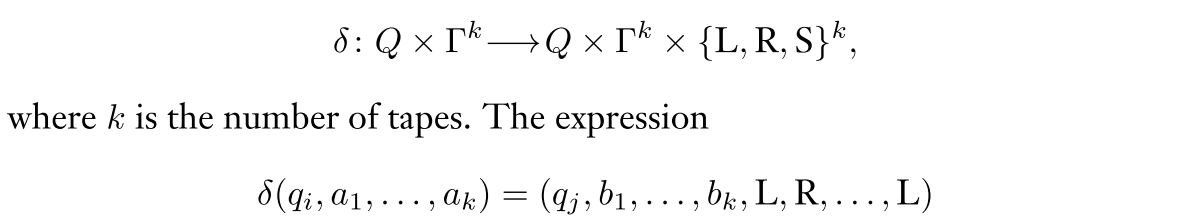
figure 3

A multi-tape TM is equivalent to a regular TM in computing power

Proof

Construct a single-tape TM that simulates (or does the exact same as a multi-tape TM).
For short, we call the single-tape TM S (for single), and the multi-tape TM M (for “multi”).

Intuition/Idea:

• We can map every tape of M to the single tape in S, and each tape content is separated by a special character: #.
• We also mark the first character of every tape string from M by a dot, like this: $\dot{w}$, to tell us where each tape starts.
• The hardest part: simulating writing characters on the tape in M. Every time a character is written on a blank space in M, it means we are appending the character on the tape, thus meaning inserting this character in the single tape of S.

S = ```

1
2
3
4
5

1. Rewrite the tape into the format \#$w_1$...$w_n$#$\dot{\sqcup}$#...$\dot{\sqcup}$#...#, a total of k $\dot{\sqcup}$'s that represent the k tapes in M.
2. In the first pass, read all the dotted symbols and pass them into the transition function, from the first # to the $k+1$th #, meaning throughout the tape. In the second pass, update the dotted symbols with what is returned by function $\delta$, particularly the part $b_1$, ..., $b_k$.
3. To simulate the movement of each head, whether going left/right/stay, go from the first $ to the $k+1$th #, remove the old dot, and then add the new dot to the new position.
4. If the head lands on the # symbol when trying to add a new dot, this action means that multi-tape M is reading on an unread blank. Therefore, S replaces the previous # symbol with blank $\sqcup$, and shifts every symbol on the right-hand side to the right one block."

Since a multi-tape TM and a single-tape TM has the same computation power, they recognize the same language. Thus we can come to the corollary: A language is Turing-recognizable if and only if a multi-tape Turing machine recognizes it.
We can also come to another corollary: A language is Turing-decidable if and only if a multi-tape Turing machine decides it.

Nondeterministic Turing Machine

A nondeterministic TM (NTM) is one that have multiple branches of transition functions, that at any point the machine may proceed according to several possibilities. The computation of an NTM is a tree with multiple branches characterized by different possible transitions, and the machine accepts the input branch that ends in $q_{accept}$.
Formally, the NTM’s transition function is defined as $\delta$(Q x $\Gamma$) $\rightarrow$ $P$(Q x $\Gamma$ x {L, R})
Here P or Greek letter Rho stands for the powerset, the all possible subset of Q, x $\Gamma$ x {L, R}, to represent all possibilities. For each combination of the current state and tape symbols, the machine can choose 0 or more possible transitions. This leads to the specialty of NTM: from one configuration, the machine can have multiple valid next steps.

This diagram shows the difference between determinism and non-determinism.

However, we can prove that an NTM and a regular TM have equivalent computing power.

Proof:

Intuition/idea:

• Since one pair of (Q, $\Gamma$) can lead to many triplets of (Q, $\Gamma$, {L, R}), we can represent these transitions into branches, using a tree data structure. Each node of the tree is a triplet of operation, (Q, $\Gamma$, {L, R}).
• ![[Pasted image 20250614121118.png]]
• an NTM can go through multiple branches of computation, but once it finds one branch getting accepted, the overall computation process ends.
• This means that we can use a tree search algorithm: either a Depth First Search (DFS) or Breadth First Search (BFS), to search for the correct branch that leads to $q_{accept}$.
  • DFS goes dives deep into one branch and returns back. Yet obviously, this is not okay: a branch can be infinitely looping, so the search will most likely miss the correct branch that accepts.
  • BFS, therefore, is suitable.
• To proof that NTM == DTM, we have to a DTM to simulate an NTM.

Constructing a multi-tape Turing machine M:
M = ```”

1. Assuming the next layer of the tree has n nodes: copy the current tape symbols to other n - 1 tapes (since there is already one tape that has contains the input content).
2. Perform the operation of the first node on the starting tape, and the operation of every other n - 1 node on the following available tapes.
3. If one of the n tape ends up in $q_{accept}$, accept.
4. Else, go to stage 1.

“
```